
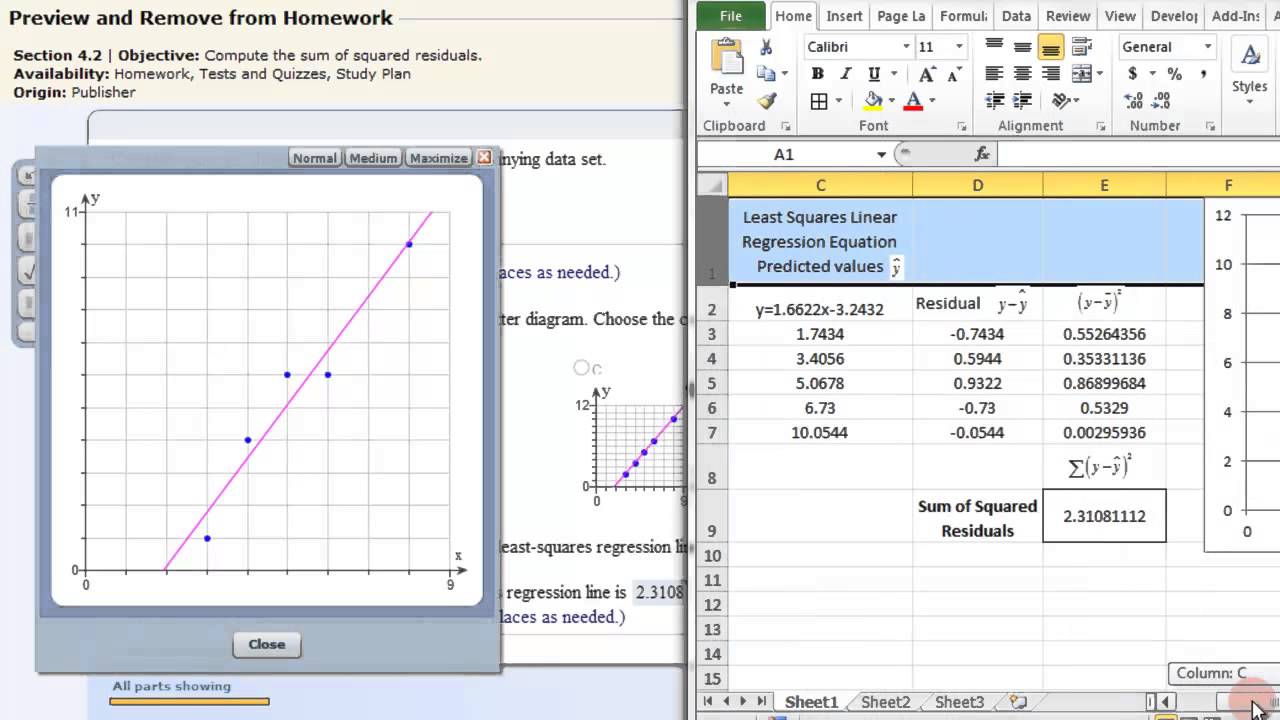
The following equations were applied to calculate the various statistical parameters: The graph below shows the linear relationship between the Mg.CaO taken and found experimentally with equation y = -0.2281 + 0.99476 x for 10 sets of data points. In a study on the determination of calcium oxide in a magnesite material, Hazel and Eglog in an Analytical Chemistry article reported the following results with their alcohol method developed: This is illustrated in an example below.Īnother approach is to evaluate any significant difference between the standard deviation of the slope for y = a + bx and that of the slope for y = bx when a = 0 by a F-test. One of the approaches to evaluate if the y-intercept, a, is statistically significant is to conduct a hypothesis testing involving a Student’s t-test. However, we must also bear in mind that all instrument measurements have inherited analytical errors as well. In my opinion, this might be true only when the reference cell is housed with reagent blank instead of a pure solvent or distilled water blank for background correction in a calibration process. Most calculation software of spectrophotometers produces an equation of y = bx, assuming the line passes through the origin. In theory, you would use a zero-intercept model if you knew that the model line had to go through zero. The questions are: when do you allow the linear regression line to pass through the origin? Why don’t you allow the intercept float naturally based on the best fit data? How can you justify this decision?

The slope of the line becomes y/ x when the straight line does pass through the origin (0,0) of the graph where the intercept is zero. A linear regression line showing linear relationship between independent variables ( x’s ) such as concentrations of working standards and dependable variables ( y’s) such as instrumental signals, is represented by equation y = a + bx where a is the y-intercept when x = 0, and b, the slope or gradient of the line.


 0 kommentar(er)
0 kommentar(er)
